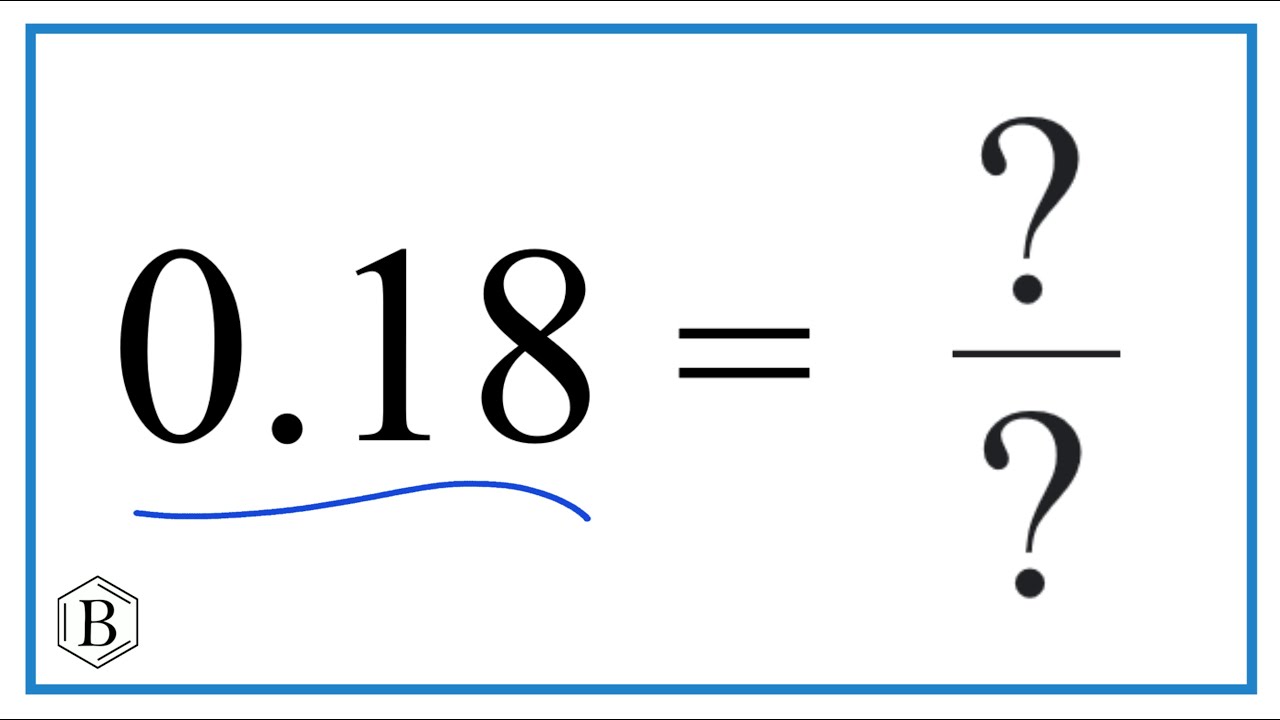When faced with the task of converting 3.6 into a fraction, one may wonder how to approach the problem. Fortunately, the process is relatively straightforward and can be broken down into a series of simple steps.
To begin, it's important to understand that 3.6 is a decimal number. Decimal numbers are numbers that contain a decimal point, which separates the whole number part of the number from the fractional part. In the case of 3.6, the whole number part is 3, and the fractional part is 0.6.
To convert a decimal number to a fraction, we need to first identify the place value of the last digit in the decimal part. In the case of 3.6, the last digit in the decimal part is 6, which is in the tenths place. This means that the fraction will have a denominator of 10.
Next, we need to determine the numerator of the fraction. To do this, we simply remove the decimal point from the decimal number and write the resulting number as the numerator. In the case of 3.6, the resulting number is 36.
Therefore, 3.6 in fraction form is 36/10. This fraction can be simplified by dividing both the numerator and the denominator by 2, resulting in the fraction 18/5.
Converting 3.6 to a fraction is a useful skill to have, as it allows us to work with decimal numbers in a more flexible way. Fractions can be added, subtracted, multiplied, and divided just like whole numbers, making them a valuable tool for solving a variety of mathematical problems.
3.6 in fraction form
When converting 3.6 to a fraction, it's important to consider the following key aspects:
- Decimal notation
- Place value
- Numerator
- Denominator
- Simplification
- Equivalence
- Applications
Understanding these aspects will help ensure a thorough understanding of the process of converting 3.6 to a fraction. For example, recognizing the place value of the last digit in the decimal part (tenths place in the case of 3.6) is crucial for determining the denominator of the fraction (10 in this case). Additionally, understanding the concept of equivalence (36/10 = 18/5) is essential for simplifying the fraction to its lowest terms.
Overall, these key aspects provide a comprehensive framework for understanding the conversion of 3.6 to a fraction. By considering each aspect carefully, individuals can develop a strong foundation in this mathematical concept and its applications.
1. Decimal notation
Decimal notation is a system for representing numbers using a radix of 10. In this system, each digit represents a power of 10, with the rightmost digit representing the ones place, the next digit to the left representing the tens place, and so on. For example, the number 365 in decimal notation represents 3 hundreds, 6 tens, and 5 ones, or 3 x 102 + 6 x 101 + 5 x 100.
- Place value
In decimal notation, each digit has a place value that determines its contribution to the overall value of the number. The place value of a digit is determined by its position within the number, with the rightmost digit having a place value of 100, the next digit to the left having a place value of 101, and so on. For example, in the number 365, the 3 has a place value of 102, the 6 has a place value of 101, and the 5 has a place value of 100.
- Decimal point
The decimal point is a symbol that is used to separate the whole number part of a number from the fractional part. The fractional part of a number represents the part of the number that is less than one. For example, in the number 3.6, the 3 is the whole number part and the 6 is the fractional part.
- Converting decimals to fractions
Decimals can be converted to fractions by dividing the numerator by the denominator. The numerator is the whole number part of the decimal, and the denominator is the number 1 followed by as many zeros as there are decimal places. For example, the decimal 3.6 can be converted to the fraction 36/10.
- Converting fractions to decimals
Fractions can be converted to decimals by dividing the numerator by the denominator. The result of the division will be a decimal number. For example, the fraction 36/10 can be converted to the decimal 3.6.
Decimal notation is a powerful tool that can be used to represent a wide range of numbers. It is the most commonly used system for representing numbers in the world today.
2. 3.6 in Fraction Form and Place Value
The concept of place value plays a crucial role in understanding 3.6 in fraction form. Place value refers to the value of a digit based on its position within a number. In the decimal system, each digit holds a value that is determined by its position relative to the decimal point. The digit to the left of the decimal point represents the whole number, while the digits to the right of the decimal point represent the fractional part.
To convert 3.6 to fraction form, we need to identify the place value of each digit in the decimal number. In 3.6, the 3 is in the ones place, and the 6 is in the tenths place. This means that the 3 represents 3 whole units, and the 6 represents 6 tenths of a unit. To convert this to a fraction, we can write 3.6 as 3 + 0.6. The whole number part, 3, can be expressed as the fraction 3/1. The decimal part, 0.6, can be expressed as the fraction 6/10. Therefore, 3.6 in fraction form is 3/1 + 6/10.
Understanding place value is essential for converting decimals to fractions and performing other mathematical operations involving decimals. It allows us to break down decimal numbers into their component parts and represent them in a more meaningful way.
3. Numerator
In the context of "3.6 in fraction form," the numerator plays a crucial role in representing the fractional part of the number. The numerator is the top number in a fraction, and it indicates how many parts of the whole are being considered. In the case of 3.6, the numerator is 6, which means that we are considering 6 tenths of the whole.
- Definition and Representation: The numerator is the number above the fraction bar in a fraction. It represents the number of equal parts that are being considered out of the total number of parts in the whole.
- Relationship to Decimal Notation: In the case of 3.6, the numerator (6) corresponds to the digit in the tenths place (0.6). This highlights the connection between the fractional part of a decimal number and the numerator of its equivalent fraction.
- Simplifying Fractions: The numerator and denominator of a fraction can be simplified by dividing both numbers by their greatest common factor (GCF). This process reduces the fraction to its lowest terms, making it easier to work with.
- Applications: Numerators are essential for performing various mathematical operations involving fractions, such as addition, subtraction, multiplication, and division. Understanding the role of the numerator is crucial for solving fraction-based problems accurately.
In summary, the numerator in "3.6 in fraction form" (6) represents the number of tenths being considered. It is an integral part of the fraction that helps us understand the fractional value of 3.6 and perform mathematical operations involving fractions.
4. Denominator
In the context of "3.6 in fraction form," the denominator plays a crucial role in representing the whole or the total number of parts being considered. It is the bottom number in a fraction and indicates the size of each individual part. In the case of 3.6, the denominator is 10, which means that the whole is divided into 10 equal parts, and we are considering 6 of those parts.
The denominator has several key aspects that contribute to our understanding of fractions:
- Definition and Representation: The denominator is the number below the fraction bar in a fraction. It represents the total number of equal parts that make up the whole.
- Relationship to Decimal Notation: In the case of 3.6, the denominator (10) corresponds to the place value of the last digit (tenths). This demonstrates the connection between the decimal notation and the denominator of its equivalent fraction.
- Simplifying Fractions: The denominator and numerator of a fraction can be simplified by dividing both numbers by their greatest common factor (GCF). This process reduces the fraction to its lowest terms, making it easier to work with.
- Applications: Denominators are essential for performing various mathematical operations involving fractions, such as addition, subtraction, multiplication, and division. Understanding the role of the denominator is crucial for solving fraction-based problems accurately.
In summary, the denominator in "3.6 in fraction form" (10) represents the total number of equal parts into which the whole is divided. It is an integral part of the fraction that helps us understand the fractional value of 3.6 and perform mathematical operations involving fractions.
5. Simplification
Simplification, in the context of "3.6 in fraction form," refers to the process of reducing a fraction to its simplest or lowest terms. This involves finding the greatest common factor (GCF) of the numerator and denominator and dividing both numbers by that factor. Simplification is important for several reasons:
- Clarity and Understanding: A simplified fraction is easier to understand and work with. It provides a clear representation of the fractional value without any unnecessary complexity.
- Mathematical Operations: Simplification is essential for performing mathematical operations involving fractions, such as addition, subtraction, multiplication, and division. It ensures that the calculations are accurate and efficient.
- Equivalence: Simplifying a fraction does not change its value. The simplified fraction is equivalent to the original fraction, but it is expressed in its simplest form.
For example, consider the fraction 36/100. The GCF of 36 and 100 is 4. Dividing both the numerator and denominator by 4 gives us the simplified fraction 9/25. This simplified fraction is equivalent to 36/100, but it is easier to work with and understand.
Simplification is a fundamental concept in working with fractions. It helps us to represent fractions in their simplest form, making them easier to understand, compare, and manipulate. A clear understanding of simplification is essential for proficiency in fraction-based mathematics.
6. Equivalence
In the context of "3.6 in fraction form," equivalence plays a crucial role in understanding the concept of fractions and their representation. Equivalence refers to the relationship between two fractions that have the same value, even though they may look different. Exploring the connection between equivalence and "3.6 in fraction form" provides a deeper understanding of fractions and their applications.
- Definition and Representation: Equivalence in fractions means that two fractions represent the same value or quantity, despite having different numerators and denominators. For example, the fractions 3/6, 2/4, and 1/2 are all equivalent to each other, as they all represent the same value of one-half.
- Simplifying Fractions: Equivalence is closely linked to the process of simplifying fractions. When we simplify a fraction, we are essentially finding an equivalent fraction that has a smaller numerator and denominator. For instance, the fraction 6/12 can be simplified to 1/2 because both fractions are equivalent and represent the same value.
- Comparing Fractions: Equivalence allows us to compare fractions and determine if they are equal or not. By finding equivalent fractions with the same denominator or numerator, we can easily compare their values and establish their relationship. For example, to compare the fractions 1/3 and 2/6, we can find an equivalent fraction for 1/3 with a denominator of 6, which is 2/6. This shows that the two fractions are equivalent and represent the same value.
- Applications in Real-Life Situations: Equivalence of fractions has practical applications in various real-life situations. For instance, in cooking, when a recipe calls for a specific fraction of an ingredient, we can use an equivalent fraction to adjust the quantity based on the availability of ingredients. Additionally, in finance, equivalence is used to compare interest rates and loan terms to make informed decisions.
In summary, equivalence is a fundamental concept in understanding fractions and their applications. By recognizing the equivalence between different fractions, we can simplify them, compare them, and utilize them effectively in various real-life situations. The connection between equivalence and "3.6 in fraction form" highlights the importance of this concept in representing and manipulating fractions accurately.
7. Applications
Exploring the connection between "Applications" and "3.6 in fraction form" reveals the practical significance and diverse use cases of fractions in various fields. Fractions play a crucial role in representing and manipulating quantities, making them essential tools in many real-life scenarios.
- Measurement and Calculations: Fractions are widely used in measurement and calculations, enabling precise representation of fractional parts of units. For instance, in carpentry, fractions are used to measure and cut wood to specific lengths, ensuring accuracy and precision in construction projects. Similarly, in cooking, recipes often involve ingredients measured in fractions, allowing for precise control over quantities and consistent results.
- Ratios and Proportions: Fractions are essential for expressing ratios and proportions, which are fundamental concepts in fields like science, engineering, and finance. For example, in chemistry, fractions are used to represent the proportions of different elements in a compound, providing insights into its composition and properties. In finance, fractions are used to compare interest rates, loan terms, and investment returns, enabling informed decision-making.
- Probability and Statistics: Fractions play a significant role in probability and statistics, where they are used to represent the likelihood of events and analyze data. For instance, in genetics, fractions are used to calculate the probability of inheriting specific traits, aiding in genetic counseling and medical research. In quality control, fractions are used to express the proportion of defective items in a batch, helping manufacturers maintain product quality.
- Geometry and Art: Fractions are also used in geometry and art to represent fractional parts of shapes and objects. For example, in architecture, fractions are used to design and construct buildings with specific proportions, ensuring aesthetic appeal and structural integrity. In art, fractions are used to create patterns, mosaics, and other designs, allowing artists to express their creativity and precision.
In summary, "3.6 in fraction form" highlights the versatility and applicability of fractions in various fields. Whether it's precise measurement, accurate calculations, or expressing ratios and proportions, fractions serve as powerful tools for representing and manipulating quantities, making them essential for solving problems and gaining insights across a wide range of disciplines.
FAQs on "3.6 in Fraction Form"
This section addresses frequently asked questions and misconceptions regarding "3.6 in fraction form" to enhance understanding and clarify common doubts.
Question 1:How do I convert 3.6 to fraction form?
To convert 3.6 to fraction form, follow these steps:
1. Write 3.6 as a fraction with 1 as the denominator: 3.6 = 36/10.
2. Simplify the fraction by dividing both the numerator and the denominator by their greatest common factor (GCF), which is 2: 36/10 2/2 = 18/5.
Question 2:Is 3.6 always equivalent to 18/5?
Yes, 3.6 is always equivalent to 18/5 in fraction form. This is because 18/5 is the simplest form of the fraction, meaning that the numerator and denominator have no common factors other than 1. Therefore, 3.6 and 18/5 represent the same fractional value.
Question 3:Why is it important to simplify fractions?
Simplifying fractions is important for several reasons:
1. Clarity and Understanding: Simplified fractions are easier to understand and work with, as they represent the fraction in its most basic form.
2. Mathematical Operations: Simplification is crucial for performing mathematical operations involving fractions, such as addition, subtraction, multiplication, and division. It ensures accurate and efficient calculations.
3. Equivalence: Simplifying a fraction does not change its value, but it makes it easier to compare and relate to other fractions.
Question 4:Can I use a calculator to convert 3.6 to a fraction?
Yes, you can use a calculator to convert 3.6 to a fraction. Simply enter 3.6 into the calculator and then press the "fraction" button (usually denoted by a fraction symbol). The calculator will display the equivalent fraction, which is 18/5.
Question 5:Where are fractions commonly used?
Fractions have a wide range of applications in various fields, including:
1. Measurement and Calculations: Fractions are used to represent fractional parts of units, enabling precise measurements and calculations.
2. Ratios and Proportions: Fractions are essential for expressing ratios and proportions, which are fundamental concepts in science, engineering, and finance.
3. Probability and Statistics: Fractions are used to represent probabilities and analyze data, aiding in decision-making and understanding statistical information.
4. Geometry and Art: Fractions are used to represent fractional parts of shapes and objects, contributing to the design and creation of artwork and architecture.
In summary, understanding "3.6 in fraction form" involves converting decimal numbers to fractions, recognizing their equivalence, and appreciating their significance in various practical applications.
Transition to the Next Article Section:
This concludes the FAQ section on "3.6 in Fraction Form." For further exploration, the next section will delve into the historical context and evolution of fractions, shedding light on their origins and development over time.
Conclusion on "3.6 in Fraction Form"
In exploring "3.6 in fraction form," we have gained a comprehensive understanding of converting decimals to fractions, recognizing their equivalence, and appreciating their significance in various practical applications. The concept of fractions extends beyond mere mathematical representation; it is a powerful tool that enables us to measure, compare, analyze, and design with precision.
The ability to convert between decimal and fraction forms is a fundamental skill in mathematics. It allows us to seamlessly navigate between different numerical representations and perform calculations efficiently. Moreover, understanding the equivalence of fractions empowers us to simplify complex expressions, identify patterns, and make informed decisions.
The applications of fractions are far-reaching, encompassing fields such as measurement, ratios, probability, geometry, and art. Fractions enable us to represent fractional parts of units accurately, express proportions and relationships clearly, calculate probabilities and analyze data effectively, design objects and structures with precision, and create visually appealing artwork.
In conclusion, "3.6 in fraction form" serves as a gateway to a deeper understanding of fractions and their multifaceted applications. By mastering these concepts, we equip ourselves with a valuable tool that empowers us to solve problems, make informed decisions, and appreciate the beauty and elegance of mathematics in the world around us.